§7 ドーム構造外論？
自閑亭のご主人のユニークな発想に刺激を受けて、直感的な Geodesic Dome 構造（以下、断りなしにドーム構造と言えばこれを指すことにします）の説明は出来ないものかと思い、ちょっと違った方向からドーム構造にアプローチしてみようと思います。どこまでうまくいくか分かりませんが、取敢えず始めることにします。
最初に断っておきますが､ここで説明する内容には､これまで説明してきた以上の情報は何もありません。そのかわり､ペーパーモデルを実際に作りながら読んでいただければ､ドーム構造を少しでも実感する参考になるのではないかと思います。
§7-1 正多面体を考える
ドーム構造は、既に説明してきた通り、正多面体構造を更に細分することによって求めています。では、その正多面体は一体何種類あるのか、考えることから始めます。
まず、平面を構成する最小の図形は、ご存知の通り３角形です。正多面体の一つの面を構成する最も単純な図形は正三角形ということになります。まず、正三角形で構成される正多面体構造を考えてみることから始めます。
多面体の一つの頂点に集まる面の数は最低３つ以上でなければなりません。もし２面ならば、二つの面が完全に重なって、ひとつの面になってしまい立体にはなりません。そこで、最も単純な構造の正多面体は、ひとつの頂点に正三角形が３面集まる構造になります。これが正４面体です。
では、頂点に集まる面の数を増やしてみます。ひとつの頂点に集まる面の数を４つにします。これが正８面体になります。更に増やして、頂点に集まる面の数を５にします。これが正２０面体になります。
それでは、ひとつの頂点に６面集まったらどうなるのか？答えは、正多面体にはなりません。正三角形の頂点の角度は６０°です。もうお分かりのように、ひとつの頂点に６面の正三角形が集まると、合計の角度は ６０°× ６ ＝ ３６０°になります。つまりひとつの平面になり、立体として閉じることが出来なくなってしまうのです。
さて、これまでのまとめをすると、
① 正多面体の頂点に集まる最低の面の数は３。
② ひとつの頂点に集まる角度の合計は３６０°を越えられない。
ということになります。この二つの条件にしたがってそのほかの正多面体を考えてみることにします。
正三角形が終わったので次は正方形です。ひとつの頂点に正方形が３面集まると、ご存知の立方体（＝正６面体）になります。ひとつの頂点に正方形が４面集まると頂点に集まる角度の合計が３６０°になってしまいます。結局、正方形で構成される正多面体は立方体ただひとつです。
次は正五角形です。正五角形の頂点の角度は１０８°です。正五角形で構成される正多面体は、ひとつの頂点に３面が集まる場合のただひとつです。これが正１２面体です。
次は正六角形です。正六角形の頂点の角度は１２０°です。ひとつの頂点に３面集まると角度の合計は３６０°になってしまいます。つまり正六角形以上の正多角形で構成される正多面体構造は存在しません。
結局、正多面体構造は、正三角形で構成される正４面体、正８面体、正２０面体、正方形で構成される正６面体（＝立方体）、そして正５角形で構成される正１２面体のわずか５種類しかないことが分かります。
これまで説明してきたことは、模型を作れば一目瞭然です。暇つぶしにでもペーパーモデルを作ってみてください！
（2001/08/08 続く）
§7-2 正多面体から生成されるドーム構造を考える
正多面体のうち､面の形状が三角形以外の平面形状で構成された多面体は平面形状が不安定なため、三角形に分割して安定した形状に変形してやるほうが良いでしょう。分割する方法としては､対角線で分割する方法と正多角形の重心から放射状に分割する方法が考えられます。
対角線で分割する場合は､新たな頂点が増えないので､立体としての形状は変化しません。これに比べて､重心を新たに頂点に加え､この重心を外接する球面上に投影してやると、より球に近い形状を得ることが出来ます。
正６面体の場合､元になる正方形を４つの直角二等辺三角形に分割することになります。実際には直角二等辺三角形の頂点を外接球に投影するので､頂点の角度は９０度より少し小さくなります。それでも､斜辺と底辺の長さはかなり違うため､長さの長い底辺が構造的な弱点になる可能性があります。そのため､立方体はドーム構造を生成するベースとなる多面体としてはあまり適していないようです。
正１２面体の場合は､正五角形を５つの二等辺三角形に分割することになります。正五角形の場合は､二等辺三角形の頂点の角度は７２度､底角は５４度になります。頂点を外接球上に投影することで､頂点の角度は更に小さくなり､反対に底角は少し大きくなります。正６面体の場合に比べるとかなり斜辺と底辺の長さの比は１に近づきます。
正１２面体を構成するひとつの正５角形が５つの三角形に分割されるので、全体として生成された三角形で構成された多面体は６０面体になります。この６０面という数字は､ちょっと気になりませんか？実はこうして出来た６０面体は、既に説明した
ClassⅡD-2の分割パターンと全く同じものになります。
§7-3 複合多面体を考える
さて､§7-1の（外側に凸の）多面体の基本的な性質に基づいて、２種類の正多角形で構成される多面体構造を考えてみます。
前節で触れた通り､正方形をベースにすると辺長の差が大きくなるので､ここではまず正３角形と正５角形の組み合わせからはじめます。
各頂点に集まる面のパターンが全ての頂点で同じになる組み合わせは､正三角形３面と正５角形１面の組み合わせと、正三角形２面と正５角形２面が交互に並ぶパターンの２種類になります。
このうち､正三角形３面と正５角形１面の組み合わせの場合､正５角形の重心を外接球に投影することによって得られる多面体は、正２０面体になります。ここでは正三角形２面と正５角形２面が交互に並ぶパターンを下図に示しておきます。
この多面体の５角形の重心を外接球上に投影する事によって得られる多面体は、８０面体になります。これは､
ClassⅠD-2の分割パターンと同じになります。
次に､正三角形と正六角形の組み合わせについて考えてみます。この場合は、各頂点に集まる面のパターンが全ての頂点で同じになる組み合わせは､正三角形３面と正六角形１面の組み合わせだけになりますが､正六角形の重心を球面上に投影して得られる二等辺三角形は底辺と斜辺の辺長がかなり差があるため､あまり実用的ではありません。
最後に､正５角形と正六角形の組み合わせについて考えます。この場合は、各頂点に集まる面のパターンが全ての頂点で同じになる組み合わせは､正５角形１面と正６角形２面の組み合わせになります。
これはご存知のサッカーボールのパターンです。正５角形と正六角形の重心を外接球上に投影して得られる多面体は、１８０面体になります。これは､
ClassⅠD-3の分割パターンです。
このように､実用的なドーム構造の分割パターンは、正２０面体を基本とした、ClassⅠ、ClassⅡの分割パターンでほとんど網羅されていると言ってよいでしょう。
（2001/08/17 続く）
§7-4 ClassⅠ D-3 を考える
最もよく知られたドーム形式として、ClassⅠD-3について、少し詳しく見ていくことにします。多少数式が出てきますが、中学生程度の平面幾何の知識があれば十分理解できると思います。実際にペーパーモデルを作りながら読んでください。
サッカーボールのパターンは、辺の長さが同じ正５角形１２枚と正六角形２０枚を作ると組み立てることが出来ます。
（１）『5/8』、『3/8』とは何？
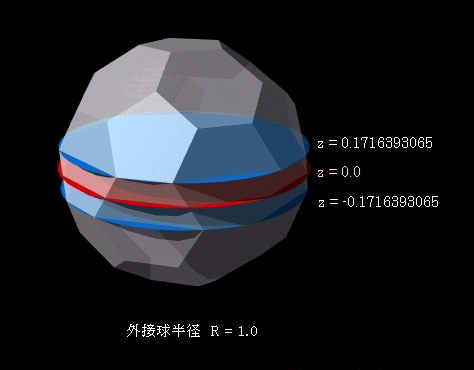
ドームのタイプで、『5/8』、『3/8』という分数を見かけることがあります。下の図に外接球の半径を1.0とした場合のサッカーボールのパターンを示しています。赤で示した平面は z = 0.0 なので外接球の赤道面を示しています。赤道面は外接球の大円になっていますから、その半径は1.0です。
この赤道面に平行で、z軸方向に±0.1716393065だけ離れた平面を考えます。z=0.1716393065から上方の部分を使ったドームを『3/8』と呼び、同じくz=-0.1716393065から上方の場合を『5/8』と呼びます。この3/8、5/8の由来は、球全体に対するドームとして使用する部分の体積比の概数で、あまり重要な意味はありません。
z=±0.1716393065で球に内接し赤道面に平行な平面の半径は以下のとおりです。
sqrt( 1.02 - 0.17163930652 ) = 0.985159859
（２）正六角形を３角形に分割する
正５角形と正六角形を張り合わせると取敢えずサッカーボールのパターンを作れます。では、出来たサッカーボールの外接球の半径は幾らになり、更に分割した３角形の大きさは幾らになるのかを考えることにします。以下、正五角形と正六角形の一辺の長さを1.0として説明します。
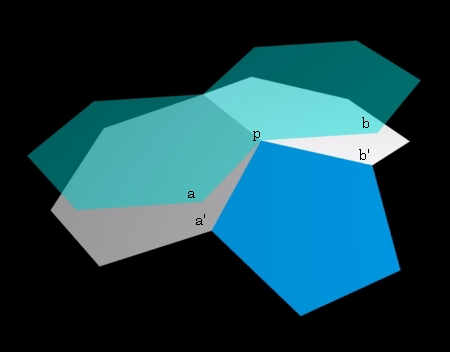
まず、一つの頂点に集まる一つの正５角形と二つの正六角形について考えます。
二つの正六角形が一つの平面上にあれば、正５角形との間に隙間ができてしまいますから、正六角形同士が接している辺上でいくらか折り曲げてやることが必要です。ではどのくらい折り曲げてやればよいでしょうか？
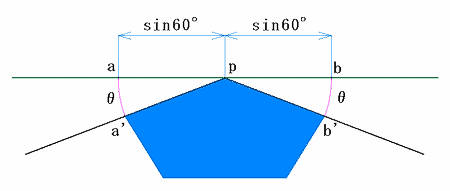
点aと点bの距離が正五角形の対角線a'b'の長さに等しくなればよいはずです。対角線a'b'の長さは、正五角形のひとつの角が108°なので、2×cos36°で求められます。正六角形同士が接している辺の延長線上から見た折れ曲がりの角度を∠apa'＝∠bpb'＝θとすると以下の通りです。
2･sin60°･cosθ = 2･cos36°= a’b’
θ = cos-1 ( cos36°/sin60°) = 20.90515745°
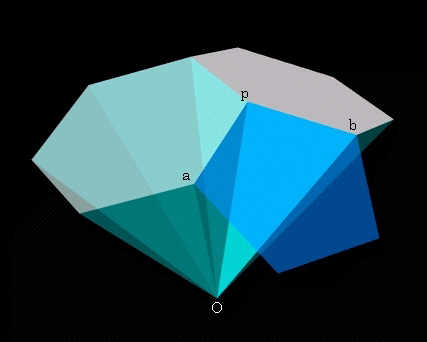
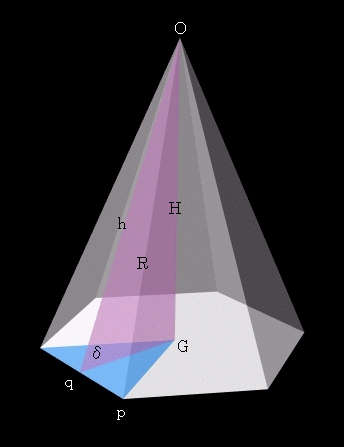
二つの正六角形を底面として、外接球の中心Oを頂点とする正六角錐を考えます。
一つの正六角錐を取り出してみます。
図のように、正六角錐の底面と側面との間の角度をδとすると、
δ = 90.0° - θ = 69.09484255°
になります。図に示す様に、正六角錐の側面を構成する二等辺三角形の高さをh、斜辺の長さをR、また、正六角錐の高さをHとします。Rは外接球半径になります。具体的に数値を求めると以下のようになります。
qG = h･cosδ
h = qG/cosδ = sin60°/cos69.09484255°= 2.427050983
R = sqrt ( (pq)2 + h2 ) = sqrt ( 0.52 + 2.4270509832 ) = 2.478018659
H = qG･tanδ = 2.267283942
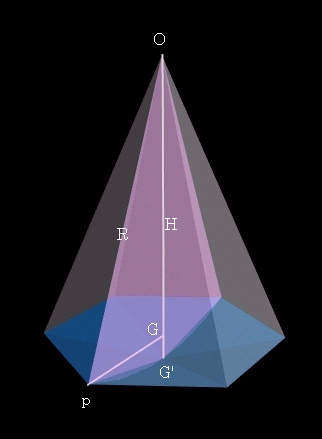
次に、正六角形の重心を外接球に投影することによって得られる二等辺三角形の斜辺長を求めます。
pG’ = L2 = sqrt ( (pG)2 + (GG’)2 ) = sqrt ( (pG)2 + (R-H)2 )
= sqrt ( 1.02 + 0.2107347172 ) = 1.021963366
になります。
ドームの場合、外接球半径を1.0として、これに対する長さをその比であらわすのが一般的です。ここでもこれに従うことにします。外接球半径 R=1.0 とした場合、正六角形から生成される二等辺三角形の底辺長および斜辺長は、以下の値になります。
L1 = 1.0/R = 0.403548212
L2 = 1.021963366/R = 0.412411489
以下、同様に正五角形から生成される二等辺三角形の斜辺長も求めることができますので、考えてみてください。
（３）例題 自閑亭たどころさんのドーム計画を検討する。
自閑亭のたどころさんは、正５角形と正六角形の組み合わせでドームの模型を作るところから設計を行っています。基礎平面は、5/8タイプなのでz=-0.1716393065の平面になります。平面形状は、ドームのベースになる正六角形の対角線と辺が交互に並んだ１０角形になります。対角線と辺の長さの比は２：１になります。
たどころさんのドームでは、元になる正五角形、正六角形の一辺の長さ（＝L1）を２３００mmとしています。これを元にそのほかの寸法を求めてみます。
まず、ドームに外接する球の半径を求めます。
R = 2300/0.403548212 = 5699.4 (mm)
次に、5/8平面の赤道面からの距離を求めてみます。
Z = -0.1716393065×R = -978.2 (mm)
5/8平面での外接円の半径は、
r = 0.985159859×R = 5614.9 (mm)
正六角形から生成される二等辺三角形の斜辺の長さは次のとおりです。
L2 = 0.412411489×R = 2350.5 (mm)
そのほかの寸法は、皆さんで考えてみてください。
ここでは、ClassⅠ D-3 ドームの注意点を述べておきます。このセクションのはじめの図を見ると、元になる正六角形の重心は3/8 あるいは 5/8 の面の上に位置しています。しかし、実際にはこの重心点は外接球の中心から球面上に投影されます。3/8 あるいは 5/8 の水平面は赤道面からずれた面であるため、正六角形の重心を球面上に投影すると、元の水平面上から少し上下にずれた位置になります。このずれを考えずにドームを組み立てようとするととんでもないことになりますので、ご注意ください！
§7-5 空間の２平面の間の角を求める
ここまでで、ドームパネルに関する外接球半径とパネルの寸法の比がどうなるかを求めることが出来ました。実際にドームを作る場合には、更に幾つかの角度を求めることが必要になります。ここでも平面幾何の知識だけで必要な角度を求めてみようと思います。
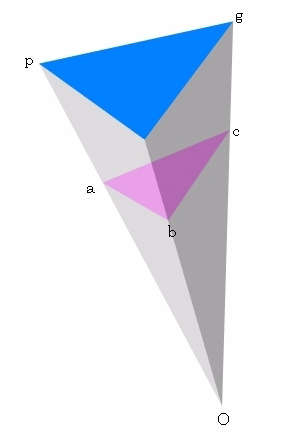
例として、正六角形から求めた一つの三角錐を取り出して考えてみます。図に示す点Oは外接球半径の中心、点ｇは元の正六角形の重心を外接球に投影して求めた頂点を示します。桃色で示した平面は、点aを通って直線Ｏｐに直交する平面を示しています。
上図に示す三角錐の側面の展開図を描いてみます。外接球に内接しているので、側面を構成する二等辺三角形の斜辺の長さは全て 1.00 になります。また三角形パネルの３辺の長さは既に求めているので展開図は下図のように容易に描くことが出来ます。
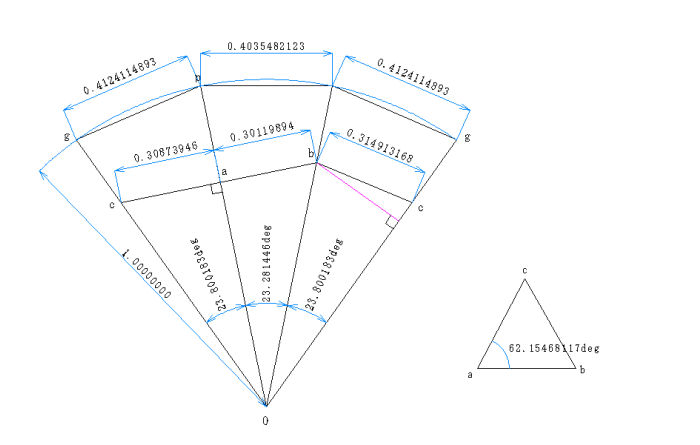
側面を構成する二等辺三角形の頂点角を求めてみます。ここでは∠gOp を求めてみます。３辺の長さがわかっているので、余弦定理から求めることができます。
∠gOp = cos-1((12+12-0.41241148932)/2/1/1) = 23.800183 deg
その他の角度も全て同様に求めることが出来ます。
さて、問題は二つの面のなす角度を求めることです。ここでは、直線Ｏｐの両側の面のなす角度を求めてみます。図の点a は点Ｏから距離０.７の点です（この距離は幾つにとってもかまいません。）。点a を通り直線Ｏｐに垂直な面と三角錐の側面との交線 ab と ac はそれぞれ直線Ｏｐに直交します。これを展開図に描きこみます。辺ｂｃも容易に描くことが出来ます。
先に求めた角度を使って、直線 ab、bc、ca の長さを求めてやります。この３辺の長さを使って三角形 abc の平面的な形状を描くことが出来ます。この三角形の頂点a の角度が求める二つの平面のなす角度になります。余弦定理より
∠cab = cos-1((0.308739462+0.301198942-0.3149131682)/2/0.30873946/0.30119894)
=62.15468117 deg.
その他の面と面のなす角度も、同じようにして全て求めることが出来ます。
