 2-1丂奣梫
2-1丂奣梫丂仒1偱 Geodesic Dome 傪掕媊偟傑偟偨丅偟偐偟偙傟偱偼Geodesic Dome偼柍悢偵懚嵼偡傞帠偵側傝傑偡偑丄幚嵺偵峔憿暔傪嶌傞応崌偵偼丄婔偮偐拲堄偡傋偒揰偑偁傝傑偡丅
倎丏Geodesic Dome傪峔惉偡傞俁妏宍偺曈偺斾偑侾偵嬤偄抣傪偲傞丅尵偄姺偊傟偽丄惓俁妏宍偵嬤偄俁妏宍偱偁傞帠丅
倐丏Geodesic Dome傪峔惉偡傞俁妏宍偺庬椶偑側傞傋偔彮側偄帠丅
丂倎偼丄椡妛揑偵傒偰僶儔儞僗偺偲傟偨峔憿偵偡傞偨傔偺忦審偱偁傝丄倐偼丄幚嵺偺晹嵽壛岺傪梕堈偵偡傞偨傔偺忦審偱偡丅偙偺俀忦審傪枮偨偡Geodesic Dome偺惗惉朄傪峫偊傑偡丅
2-2丂惓懡柺懱
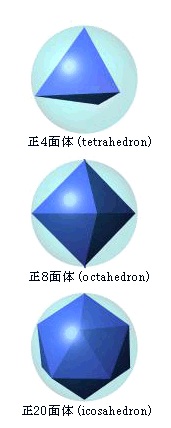
丂媴偵撪愙偡傞惓俁妏宍偱峔惉偝傟傞懡柺懱峔憿偵偼丄惓係柺懱丄惓俉柺懱偦偟偰惓20柺懱偺俁庬椶偑懚嵼偡傞偙偲偼廃抦偺偲偍傝偱偡丅
丂仒侾偺掕媊偵廬偊偽偙傟傜偺惓懡柺懱峔憿傕Geodesic Dome偺堦庬偩偲峫偊傞偙偲偑弌棃傑偡丅偟偐偟丄奜娤偐傜庴偗傞報徾偼偛偮偛偮偟偰偄偰偲偰傕僪乕儉偲偼屇傋傑偣傫丅偙偺惓懡柺懱傪傕偲偵丄傛傝媴宍偵嬤偄懡柺懱峔憿亖Geodesic Dome傪惗惉偡傞庤朄傪埲壓偵帵偟傑偡丅
2-3丂Geodesic Dome 偺惗惉
丂傑偢巒傔偵丄惓懡柺懱傪峔惉偡傞奺惓俁妏宍傪峏偵嵶偐偄惓俁妏宍偵暘妱偟傑偡丅偦偟偰丄暘妱偟偨惓俁妏宍偺捀揰偺拞偱丄奜愙媴忋偵側偄揰傪奜愙媴偺拞怱偐傜媴柺忋偵搳塭偟傑偡丅搳塭偝傟偨捀揰傪怴偨側捀揰偲偟偨俁妏宍乮昁偢偟傕惓3妏宍偵偼側傜側偄乯偵傛偭偰慡偰偺捀揰偱媴偵撪愙偡傞俁妏宍偱峔惉偝傟偨懡柺懱峔憿亖Geodesic Dome偑惗惉偝傟傑偡丅
丂偝偰丄媴柺忋偵側偄捀揰傪媴柺忋偵搳塭偡傞偙偲偵傛偭偰丄惗惉偝傟偨怴偨側俁妏宍偵偼榗傒偑惗偠偰昁偢偟傕惓俁妏宍偵偼側傝傑偣傫丅摿偵丄傕偲偵側傞惓懡柺懱偺柺悢偑彮側偄傎偳偦偺榗傒偼戝偒偔側傞偲峫偊傜傟傑偡丅偦偙偱丄幚嵺偵偼惓20柺懱傪傕偲偵偟偰Geodesic Dome傪惗惉偡傞偙偲偵偟傑偡丅
丂惓懡柺懱傪峔惉偡傞惓俁妏宍偺暘妱曽朄偵傛偭偰擇偮偺Geodesic Dome宯偑峫偊傜傟傑偡丅埲壓偵偦傟偧傟偵偮偄偰愢柧偟傑偡丅
2-3-1丂Class嘥

丂嵟傕帺慠側暘妱曽朄偼丄惓20柺懱傪峔惉偡傞惓俁妏宍偺俁曈傪摍暘妱偟偰丄偙偺揰傪捠傝奺曈偵暯峴側捈慄偱暘妱偡傞曽朄偱偡丅偙偺暘妱偵傛偭偰惗惉偝傟傞宯傪Class嘥偲屇傇偙偲偵偟傑偡丅恾偵丄嵟傕暘妱悢偺彮側偄俀暘妱乮Class嘥D-2乯偺惗惉夁掱傪帵偟傑偡丅
丂傑偢偼偠傔偵丄惓俁妏宍偺奺曈傪俀摍暘偟偰偙偺揰傪捠傝奺曈偵暯峴側捈慄偱暘妱偡傞偙偲偵傛偭偰係偮偺惓嶰妏宍偵暘妱偟傑偡丅
丂師偵丄奜愙媴忋偵側偄惓俁妏宍偺捀揰傪媴偺拞怱偐傜媴柺忋偵搳塭偟傑偡丅偦偟偰搳塭偝傟偨捀揰傪俁妏宍偺捀揰偲偡傞怴偨側俁妏宍傪惗惉偟傑偡丅
丂惓20柺懱傪峔惉偡傞慡偰偺柺偵懳偟偰摨偠憖嶌傪偡傞偙偲偵傛偭偰Class嘥D-2偺姰慡側懡柺懱峔憿偑惗惉偝傟傑偡丅
丂偙偆偟偰惗惉偝傟傞Geodesic Dome偺柺偺悢偼堦曈偺暘妱悢傪値偲偡傞偲20値亊値柺偵側傝傑偡丅値亖俀偺応崌偼80柺懱偱偡丅
丂値亖俀偺応崌丄搳塭偺懳徧惈偐傜愒偔帵偟偨柺偼惓俁妏宍偵側傝丄惵偱帵偟偨嶰偮偺俁妏宍偼俀摍曈俁妏宍偵側傝傑偡丅