§８　空間幾何概説

８−１　はじめに

　このセクションでは、ドームハウスの設計に必要十分な空間幾何の理論について簡単に説明します。ただし、論理的な厳密さは省略しますので、必要ならば、高校の幾何の教科書などが役に立つと思います。
　ここでは、オンラインソフトとして配布しているDomeDesign.exeが使用できることを前提に説明を進めることにします。このセクションでは、正２０面体（Icosahedron）を例題とします。

　まずはじめに、DomeDesignを起動して、DesignメニューからGeodesic Domeを選択します。



ここで、ドームタイプとしてIcosahedronを選択し、executeボタンを押します。Node No.チェックボックスにチェックを入れてdrawボタンを押すと正２０面体をz軸方向から見た図が表示されます。次に、Printoutグループで、R=1000000を指定して座標値ボタンを押すと以下の結果が印刷されます。

******** Geodesic Dome Peak Point Coordinate ********
        ( Dome Type : D-1  R = 1000000.00 )

node No.     * x *           * y *           * z *
    1           0.000           0.000     1000000.000
    2      894427.191           0.000      447213.595
    3      276393.202      850650.808      447213.595
    4     -723606.798      525731.112      447213.595
    5     -723606.798     -525731.112      447213.595
    6      276393.202     -850650.808      447213.595
    7      723606.798      525731.112     -447213.595
    8     -276393.202      850650.808     -447213.595
    9     -894427.191           0.000     -447213.595
   10     -276393.202     -850650.808     -447213.595
   11      723606.798     -525731.112     -447213.595


　各数値をRで割って正規化すると、半径1.0の球に内接する正２０面体の頂点座標を得ることができます（はじめからR=1.0とすると、有効数字が３桁しか取れないので角度計算において少し精度が足りません）。これで、正２０面体の頂点座標の準備ができました。
(2002/02/24)
８−２　幾何ベクトル

　ベクトルあるいはベクトル量とは、大きさと方向を持つ物理量です。例えば速度、加速度、力などがこれにあたります。幾何ベクトルとは、幾何学的な位置関係を表すベクトルです。以下ここでは特に説明の無い限り、ベクトルといえば幾何ベクトルをさすことにします。


　上の図は、正２０面体を構成する正３角形のひとつを示しています。点p1,p2,p3は前のセクションで示した正２０面体の頂点の１から３に対応します。ただし、一般性を持たせるために、半径Rで座標値を正規化しています。各点の座標値は以下のとおりです。

            * x *           * y *           * z *
    p1      0.0              0.0             1.000000000
    p2      0.894427191      0.0             0.447213595
    p3      0.276393202      0.850650808     0.447213595

　さて、図に示す原点から各点に向かう青で示した有向線分はベクトルを表し、特に原点をベクトルの始点として、空間の任意点に向かうベクトルだということから「位置ベクトル」と呼びます。位置ベクトルの要素はベクトルの終点の座標値になります。したがって、p1,p2,p3の位置ベクトルは以下のとおりです。

　以下、ベクトルは太文字の小文字で表記することにします。p1,p2,p3の位置ベクトルはそれぞれ p1, p2, p3 と表すことにします。

　ベクトルには、大きさと方向があることを既に述べました。ベクトル v = ( x , y , z ) の大きさは各要素の二乗和の平方根によって求めます。

　これは、ベクトルの長さを表します。位置ベクトルでは座標原点から終点までの距離になります。p1 について計算してみると以下のとおりです。

以下、p2, p3 についても同様に求めることができます。

　ベクトルの方向は、ベクトルのx,y,zの各要素の正負の符号と比率によって定まります。ベクトル v = ( x , y , z ) において、x,y,zの各要素をベクトルの大きさ |v| で正規化した値を方向余弦と呼びます。具体的には、
x/|v| = l , y/|v| = m , z/|v| = n

ベクトルの大きさが違っていても、方向余弦が等しいベクトルは方向が同じになります。また、方向余弦には以下の関係が成り立ちます。
l2 + m2 + n2 = 1

　あるベクトル v の要素の符号をすべて反対にしたベクトルを -v と表し、このベクトルは元のベクトルと大きさは等しく、方向が反対になります。
(2002/02/27)
８−３　ベクトルの和と差

　この節では、ベクトルの和と差を求めることを考えてみます。

ベクトルの和は、一つのベクトルの終点に加えるベクトルの始点を一致させることによって求められます。例えば、上の図において、点p1の位置ベクトル p1 に a ベクトルを加えることを考えます。p1 の終点p1に a の始点を一致させます。得られた新しいベクトル（p1+a)は、始点は座標原点であり、終点は点p2になります。これは、点p2の位置ベクトルにほかなりません。つまり、
p1 + a = p2

　さて、前節の終わりに、「あるベクトル v の要素の符号をすべて反対にしたベクトルを -vと表し、このベクトルは元のベクトルと大きさは等しく、方向が反対になります。」と述べました。このことより直ちに、
v + (-v) = v - v = 0

が導かれます（ 0 は要素がすべてゼロのベクトル）。この性質を利用すると、

p1 + a - p1 = p2 - p1　つまり　a = p2 - p1

ベクトル a の具体的な要素は p2 と p1 の差として求められることがわかります。a の意味は点p2の点p1に対する相対的な位置を表し、その大きさは点p2と点p1の距離を示します。具体的に a と b を求めると以下のようになります。

a =((0.894427191-0.0) , (0.0-0.0) , (0.447213595-1.0)) = (0.894427191 , 0.0 , -0.552786405)
b = p3 - p1 = ((0.276393202-0.0) , (0.850650808-0.0) , (0.447213595-1.0))
= (0.276393202 , 0.850650808 , -0.552786405)
|a| = |b| = 1.051462224
(2002/02/28)
８−４　ベクトルの内積（あるいはスカラー積）

　この節では、ベクトルの内積について考えます。二つのベクトル a = (a1,a2,a3), b = (b1,b2,b3)の内積は、二つのベクトルのなす角度をθとした場合、次の式で定義されます。

a・b = |a||b|cosθ = a1･b1 + a2･b2 + a3･b3

具体的な数値を入れて計算すると以下のとおりです。

a・b = 0.894427191･0.276393202 + 0.0･0.850650808 + (-0.552786405)･(-0.552786405)
= 0.552786405

内積を計算することによって、a と b のなす角度を次の式で求めることができます。

θ = cos-1(a・b/(|a||b|))

数値を代入して実際の角度を求めてみます。

θ =　cos-1(0.552786405/(1.051462224･1.051462224))　=　cos-1(0.5) = 60.0 (deg)

正２０面体を構成する３角形は正３角形なので、a と b のなす角度は60.0degになります。
(2002/03/01)
８−５　ベクトルの外積（あるいはベクトル積）

　この節では、ベクトルの外積について考えます。二つのベクトル a = (a1,a2,a3), b = (b1,b2,b3)の外積は、次の式で定義されます。

a×b = (a2b3-a3b2)i + (a3b1-a1b3)j + (a1b2-a2b1)k
= ( (a2b3-a3b2) , (a3b1-a1b3) , (a1b2-a2b1) )
　ただし、i = (1 , 0 , 0) , j = (0 , 1 , 0) , k = (0 , 0 , 1)

具体的に a×b を計算してみます。

a2b3-a3b2 = 0.0･(-0.552786405) - (-0.552786405)･0.850650808 = 0.470228202
a3b1-a1b3 = (-0.552786405)･0.276393202 - 0.894427191･(-0.552786405) = 0.341640787
a1b2-a2b1 = 0.894427191･0.850650808 - 0.0･0.276393202 = 0.760845213

∴ a×b = (0.470228202 , 0.341640787 , 0.760845213)


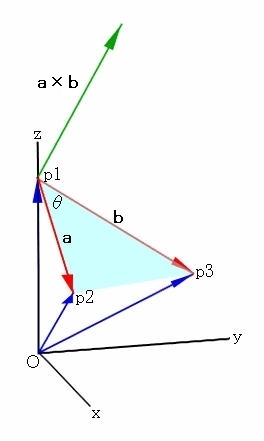
　外積の大きさには次の性質があります。

|a×b| = |a||b|sinθ　( 0deg ＜θ＜ 180deg )

　具体的に数値を代入してみると、

|a×b| = sqrt( 0.4702282022 + 0.3416407872 + 0.7608452132 ) = 0.957454139
|a||b|sinθ= 1.051462224･1.051462224･sin60゜= 0.957454138

　a×b の大きさ |a×b| は、aとbを隣接する２辺とする平行四辺形の面積（＝ a と b を２辺とする３角形の面積の２倍）に等しいことを示しています。
　a×b は、a と b に直交し（冪1p2p3に直交するベクトル、法線ベクトル）、その正方向は、a を b に重ねるようにθだけ回転するときに右ねじの進む方向になります。
(2002/03/02)
８−６　２平面のなす角

　この節では、二つの平面がなす角度を求めることを考えます。二つの平面として、冪1p2p3と儖p2p3を考えます。まず、儖p2p3の法線ベクトルを求めます。

p2×p3 = ( -0.380422606 , -0.276393202 , 0.760845213 )
|p2×p3| = 0.894427191



　上の図に、冪1p2p3と儖p2p3の法線ベクトルである a×b と p2×p3 を示します。点p2と点p3が重なって見える方向から見た図を下図に示します。



　この図は、冪1p2p3と儖p2p3の両方に直交する平面への正射影と考えることもできます。δ = ∠p1p2O は冪1p2p3と儖p2p3の二つの面のなす角度です。 a×b と p2×p3 はそれぞれ線分p1p2と線分Op2と直交しています。このことから、 a×b と p2×p3 のなす角度もδになることがわかります。
　結局、冪1p2p3と儖p2p3の二つの面のなす角度を求めるためには、それぞれの法線ベクトルである a×b と p2×p3 のなす角度を求めることになります。

δ = cos-1(((a×b)・(p2×p3))/(|a×b||p2×p3|))

(a×b)・(p2×p3)
= 0.470228202･(-0.380422606)+0.341640787･(-0.276393202)+0.760845213･0.760845213
= 0.305572809
|a×b||p2×p3| = 0.957454139･0.894427191 = 0.856373016

∴δ = cos-1(0.305572809/0.856373016) = 69.09484257 (deg)
(2002/03/04)
８−７　DomeDesign.exeを使う

　前節まで、具体的な数値を使って、多少煩雑な計算をしてきました。少し面倒だったかもしれませんが、どのようにすれば必要な数値が求められるのかを理解する上で必要なプロセスだと思います。この節では、フリーソフトとして公開しているDomeDesign.exeを使ってこれまで計算してきた例題の数値を求めます。DomeDesign.exeを使う上で、空間幾何の基礎を理解することはいろんな局面への応用で必ず役に立つと思います。

（１）空間３角形

ここでは、冪1p2p3 を例に計算してみます。


L1, L2, L3は、点p1, p2, p3の対辺の長さを示しています。α1, α2, α3は、各頂点の角度です。Vnは冪1p2p3の単位法線ベクトルです。８−５の表記を用いればVn = (a×b)/|a×b|の値です。Areaは、冪1p2p3の面積であり、Area = |a×b|/2の値です。
　この空間３角形を用いれば、ドームパネルの設計に必要な数値のうち、部材長、と角度α、βを計算することができます。

（２）２面間角度

　ここでは、冪1p2p3と儖p2p3の二つの面の角度を例に計算してみます。



　２面間角度の計算を用いれば、角度γ、δを計算することができます。
(2002/03/05)